Veja os exercícios resolvidos e aprenda como fazer!
Exercicios sobre função
Profa.
Rosana G. S. Miskulin
- Sendo f(x) = x / (x+1), g(x) = x10 e h(x) = x +3
Escrever:
f o g o h (x) =?
f
o g o h (x) = f (g (h(x) ) ) = f ( g (x +3 ) ) =
f
( (x +3 )
10
) = (x
+3 )
10
/ (x +3 )
10 +1
- Sendo f(x) = x2 , g(x) = cosx e h(x) = x + 9
Escrever:
f o g o h (x) = f (g (h(x) ) ) =
f ( g (x + 9 ) ) = f ( cós (x +
9) ) = [cós
( x + 9) ]2
- Sendo f(x) = x -7, g(x) = x2 e h(x) = x +3
Escrever:
f (g(x) ) = f (x2)
= x2-7
e
f (g(2) ) = 4 - 7 = -
3
- Sendo f(x) = x + 5, g(x) = x2 - 3, calcular:
a)
f (g(0) ) =
b)
g (f(0) =
c)
f(g(x)) =
d)
g(f(x)) =
e)
f(f(-5) ) =
f)
g (g(2) ) =
g)
f(f(x)) =
h)
g(g(x) ) =
Solução:
a)
f(g(0))
g(x)
= x2
– 3, portanto g(0) = 0 - 3 = -3 e f(x) = x + 5, portanto
f(g(0))
= f(-3) = -3 + 5 = 2
b)
g(f(0))
f(0) =
0 + 5 = 5, portanto g(f(0)) = g(5) = 52
– 3 = 25 – 3 = 22
c)
f(g(x))
g(x) =
x2 –
3, portanto f(g(x)) = f(x2
– 3) = x2
– 3 + 5 = x2
+ 2
d)
g(f(x))
f(x)
= x + 5, portanto g(f(x)) = g(x + 5) = (x + 5)2
– 3 = x2
+ 10x + 25 – 3 = x2
+ 10x + 22
e)
f(f(-5))
f(-5) =
x + 5 – 5 = 0, portanto f(f(-5)) = -5 + 5 + 5 = 5
f)
g(g(2))
g(2) =
22 –
3 = 4 – 3 = 1, portanto g(g(2)) = g(1) = 12
– 3 = 1 – 3 = -2
g)
f(f(x))
f(x) =
x + 5, portanto f(f(x)) = f(x + 5) = x + 5 + 5 = x + 10
h)
g(g(x))
g(x)
= x2
– 3, portanto g(g(x)) = g(x2
– 3) = (x2
– 3)2
– 3 = x4
– 6x2
+ 9 – 3 = x4
– 6x2
+ 6
5)
Sendo f(x) = x -1, g(x) = 1 / (x+1)
Escrever:
a) f (g(x) ) = f(1 / (x+1) ) = 1
/ (x+1) -1
b) f (g(1/2) )= 1 / [(x+1) -1] = 1 / (1/2+1)=
-1/3
c)
g( f (x) ) = g (x -1) =1 / [(x -1)+1] =
1
/ x -1+1 = 1/x
d)
g( f (2) ) =1/2
e)
f (f (x) ) = f(x -1) = (x -1) -1 = x
-2
f)
g ( g (2) ) = g [1 / (x+1) ] = 1 / ([1 / (x+1)]+1) =(x+1) / ( x+2) =
3/4
- f ( f(2) ) = x -2 = 0
6)
Encontrar o coeficiente angular e o coeficiente linear da reta: 8x +
5y = 20. Represente
a reta gráficamente.
5y
= 20 - 8x
y = (20 - 8x) / 5 y
= 20/5 – 8/5x
y = 4 - 8/5x ou
y = - 8/5x + 4
m
= -8/5 e b = 4
7)
Escrever uma equação para a reta que passa pelo ponto (-1, -3) e
que seja :
- paralela à reta L: y = 3x - 4
- perpendicular à reta L: y = 3x – 4
- ponto (-1, -3) e paralela à reta L: y = 3x - 4
(m = 3)
y – y1
= m (x- x1
)
y + 3 = 3 ( x +1)
y + 3 = 3x +3
y = 3x + 3 -3
y
= 3x
- ponto (-1, -3) e perpendicular à reta ( m = -1/3)
L: y = 3x – 4
y – y1
= m (x- x1
)
y + 3 = -1/3 ( x +1)
y + 3 =
-1/3 x - 1/3
y = -1/3x - 1/3 - 3
y = -1/3x
-10/3
8)
Escrever uma equação para a reta que passa por P que é:
- paralela à L e
- perpendicular à L
- P (0, 0 ) e L: y = -x + 2
- P ( -2, 2) e L: 2x + y = 4
a) P (0, 0 ) e L: y = -x + 2
i) paralela à L: y = -x + 2
a) P (0, 0 )
e L: y = -x + 2 (m = -1)
y – y1
= m ( x-x1)
y – 0 = -1
( x – 0) y
= -x
ii)
perpendicular à L
( m= 1)
y – y1
= m ( x-x1)
y – 0 = 1
( x – 0) y
= x
- P( -2, 2) e L: 2x + y = 4y = 4 – 2x ou y = -2x +4
- paralela à L ( m = -2)
y – y1
= m ( x-x1)
y – 2 = -2
( x – 0) y-2
= -2x
y
= -2x +2
ii)
perpendicular à L (m = +1/2)
y – y1
= m ( x-x1)
y – 2 =
+1/2 ( x – 0)
y-2
= +1/2x
y
= +1/2x + 2
9)
Dizer se a função é par ou impar?
- f(x) = 3 f é constante
f(-x)
= 3 logo f(x) = f(-x) f é par
b) f(x) = x
-5
f(-x) = (-x)
-5
= 1/ (-x)
5
= 1/ -x5
= - x -5
logo f(-x) = - f(x) , logo f
é impar.
10)
Dizer se a função é par ou impar?
a)
y = x2
+1
f(-x)
= (-x)2
+1 x2
+1 = f(x)
f é par
- y = x2 +x
f(-x)
= (-x)2
+(-x) x2
- x = f(x)
f não é par e nem impar
11)
Dizer se a função é par ou impar?
- g(x) = x3 +x
g ( -x) = (-x)
3 +
(-x) = -x3
–x = -( x3
+x) = - g(x)
f é impar
- g(x) = x4 – 3x2 – 1
- g(-x) = (-x) 4 – 3 (-x) 2 -1 = x4 - 3 . x2 -1 = g(x)
f é par
12)
Dizer se a função é par ou impar?
- h(t) = 1 / (t-1)
h(-t) = 1/ ( -t -1) = 1 [-(t+1)
] =
- [1 / (t+1)
] DIFERENTE DE - h(t). LOGO
A FUNÇÃO NÃO É PAR E NEM ÍMPAR
- h(t) = | t3 |
h(-t) = |
(-t)
3
| = | -t3
| = | t3
| = h(t)
f é par
13)
Determinar a função inversa de y = 1/2x +1, expressando-a em função
de x. Depois confira o seu resultado.
1)f(x)
= y = 1/2x +1
2)
y -1 = 1/2x
x = [(y -1)] / ½ = 2y -2 x
= 2y -2
3)
trocar x por y
f-1(x)
y
= 2x -2
f
( f-1(x)
) = f (2x -2) =
x
f-1(
f(x) ) = f-1(1/2x
+1) = 2(1/2x
+1) -2 =
x
14) Determinar a função inversa
de y = x2
expressando-a
em função de x. Depois confira o seu resultado.
f(x) = x2
1)y = x2
2) x = raizq y
3) y = raizq
x = f-1(x)
f
( f-1(x)
) = f (raizq x) = (raizq x)2
= x
f-1(
f(x) ) = f-1(x2)
= raizq x2
=
x
15)
Encontre uma fórmula para a função descrita e obtenha o seu
domínio.
a)
Expresse a área de um triângulo eqüilátero como uma função do
comprimento de um dos seus lados.
Solução:
No
triângulo eqüilátero de lado l a altura h é dada por: h = l sen
60º =
l
Área
do triângulo =
Uma
vez que o lado de um triângulo não pode ser um número negativo, e
não tem restrições de tamanho, o domínio é dado por
b)
Um retângulo tem um perímetro de 20 m. Expresse a área do
retângulo como uma função do comprimento de um dos seus lados.
Solução:
O
perímetro mede 20m, portanto:
2x + 2y = 20 → x + y = 10 →
y
= 10 – x
Uma vez
que os lados do retângulo têm que ser um número positivo, 0 < x
< 10
Área
do retângulo = x.y = x.(10 – x) = -x2
+ 10x
18)
Um homem apara seu gramado toda quarta-feira à tarde. Esboce o
gráfico da altura da grama como uma função do tempo no decorrer de
um período de quatro semanas.
Para
resolver este exercício temos que assumir algumas hipóteses: 1) O
gramado é cortado sempre na mesma altura mínima. 2) Durante a
semana que separa cada corte o gramado cresce sempre na mesma
proporção, atingindo portanto a mesma altura máxima. 3) Vamos
iniciar o gráfico no dia do corte, isto é, quarta feira.
19)
Determine o domínio e a imagem de f(x) = 2 +
Solução:
Para que a função
esteja
definida x – 1 ≥ 0, ou seja x ≥ 1, logo o domínio de f(x) = 2
+
é x pertencente aos reais, tal que x ≥ 1. Uma vez que
≥ 0 a
imagem de f(x) = 2 +
é y pertencente aos reais, tal que y ≥ 2.
20)
Determine o domínio de f(x) = (x + 1) / (x – 1)
Solução:
A função acima não está definida para x = 1. Portanto seu domínio
é x pertencente aos reais tal que x ≠ 1.
Exercícios sobre limites
Calcule os seguites limites abaixo:1-)
Resolução:
Obs:Substituindo por 2 diretamente na função fica 2*2-7*2+10/2*2-4= 4-14+10/4-4 = -10+10/4-4=0/0,isto no cálculo é chamado limite indeterminado que além de 0/0, infinto/infinito e -infinito/-infinito também são limites indeterminados, e portanto devese calcular o limte usando alguns artíficios algébricos como mostra-se na resolução do problema abaixo:
2-)
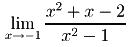
Resolução:
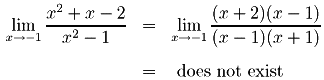
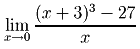
Resolução:
Fonte: http://www.mtm.ufsc.br/~azeredo/calculos/Acalculo/x/listas/limites/limite.html
Exercicios sobre derivada
NO
LIVRO DE HOWARD ANTON: CÁLCULO: um novo horizonte – Vol. 1 Páginas
186/187
Resolução
/ Explicação
RESOLUÇÃO;
F’(1)
= ?
F’(3)=
?
F’(5)
= ?
F’(6)
= ?
f’(1)
= ?
No
ponto x =1 a reta tangente à curva y = f(x) é a reta
VERMELHA.
Identifique 2 pontos quaisquer que pertençam à reta tangente à
curva y = f(x), no ponto x = 1.
Assim, os pontos são: (1,3
) e (0, 1) . Então:
y-y1
= m (x-x1)
m = y-y1
/ (x-x1)
m
= 1-3 / 0 -1 = 2
m
= 2
f’(3) = ?
No
ponto x =3 a reta tangente à curva y = f(x) é a reta
AZUL. Identifique
2 pontos quaisquer que pertençam à reta tangente à curva y =
f(x), no ponto x = 3.
Assim, os pontos são: (3, 6
) e (6, 6) . Então:
y-y1
= m (x-x1)
m = y-y1
/ (x-x1)
m
= 6 - 6 / 6 -3 = 0 / 3
m
= 0
f’(5) = ?
No
ponto x =5 a reta tangente à curva y = f(x) é a reta
VERDE.
Identifique 2 pontos quaisquer que pertençam à reta tangente à
curva y = f(x), no ponto x = 5.
Assim, os pontos são: (5, 3
) e (6, 1) . Então:
y-y1
= m (x-x1)
m = y-y1
/ (x-x1)
m
= 1-3 / 6 -5 = -2 / 1
m
= -2
f’(6) = ?
No
ponto x =6 a reta tangente à curva y = f(x) é a
reta ROSA FORTE.
Identifique 2 pontos quaisquer que pertençam à reta tangente à
curva y = f(x), no ponto x = 6.
Assim, os pontos são: (6, 1
) e (5, 2) . Então:
y-y1
= m (x-x1)
m = y-y1
/ (x-x1)
m
= 2-1 / 5 -6 = 1 / -1
m
= -1
EXRECÍCIO 3 PARTE A)
A DERIVADA É IGUAL A
INCLINAÇÃO DA RETA TANGENTE À CURVA, NO PONTO DESEJADO. PORTANTO,
CALCULARIA A INCLINAÇÃO DA RETA TANGENTE À CURVA, NO PONTO a.
ATENÇÃO
- EXERCÍCIO 3 B ( A LETRA B DESSE EXERCÍCIO NO LIVRO TEM UM
PROBLEMA - O ENUNCIADO ESTÁ ERRADO O CERTO É
Y
= 3X -
1
A EQUAÇÃO DA RETA TANGENTE
AO GRÁFICO Y = F(X) NO PONTO (2,5) É Y = 3X-1, DETERMINE
F’(2) =? A DERIVADA NO
PONTO 2????
y= f(x))
Y = 3x – 1
Como
Y
= 3x – 1 é a equação da reta tangente no ponto (2,5) pode-se
concluir que f’(2) = 3 ( coeficiente angular da reta tangente = m )
Assim,
somente olhando-se
na equação da tangente e interpretando-a
, conclui-se que:
f’(2) = 3,
que é o coeficiente angular da reta no ponto x = 2 e y = 5, no ponto
(2,5).
EXERCÍCIO 4 -
Pelos dados do exercício tem –se que A RETA
TANGENTE PASSA PELOS PONTOS: (-1, 3) E ( 0, 4)
O
ponto ( -1, 3) é um ponto que pertence
à reta tangente e à função,
pois ele é o
ponto de tangência da função com a reta tangente.
O
ponto ( 0, 4) só
pertence à reta tangente mas,
não pertence à função.
Então
tem-se no exercício 2 pontos que pertencem à reta tangente (-1, 3)
E ( 0, 4) , aplica-se a fórmula e calcula-se a inclinação da reta
tangente = m.
Assim,
m
= y-y1
/ (x-x1)
= 3 – 4 / -1 – 0 = -1 / -1 = +1, logo m
= 1
Que
é a inclinação da reta tangente, que é igual a derivada da
função no ponto (-1,3) que é o ponto de tangência , onde a reta
tangente tangencia a f(x) .
Então:
f’(-1) = m = 1
(EM GERAL, PARA CADA PONTO
DA FUNÇÃO TEM-SE UMA RETA TANGENTE DIFERENTE)
EXERCÍCIO
7
F(3)
= -1 →A FUNÇÃO PASSA PELO PONTO (3, -1)
Como
F’(3) = 5 ( a
derivada no ponto x = 3 ) Conclui-se que A DERIVADA OU A INCLINAÇÃO
DA EQUAÇÃO DA RETA TANGENTE à função y = f(x) no ponto (3, -1)
é igual a 5, ou seja:
m =5
Sabe-se
que: O ponto (3,-1) pertence à reta tangente e também pertence à
f(x)
Portanto,
a equação da reta tangente à função y = f(x) , no ponto (3,-1)
é:
y-y1
=
m (x-x1)
y +1 = 5 ( x -3) y
+1 = 5x – 15
y
= 5x -15 -1
y
= 5x - 16
EXERCÍCIO
–
8 -
(
-2, 3) pertence à função e também pertence à equação da reta
tangente
pois esse ponto é o ponto de tangência.
Sabe-se
que f’(-2)
= -4 = m
inclinação da reta tangente
coeficiente angular da reta tangente
derivada da função no ponto ( -2, 3) (ponto de tangência).
Então:
como f’(-2 ) = -4 tem-se
que: m = -4
E
como f(-2) = 3 tem-se que o ponto (-2, 3) pertence à equação da
reta tangente e também pertence à função. Aplicando-se a fórmula,
tem-se que:
y-y1
=
m (x-x1)
y
– 3 = -4 ( x +2) y
= -4x - 8 +3
y
= -4x -5
EXERCÍCIO
–
9- RESPOSTA:
Y = 18X – 27
EXERCÍCIO
–
10- RESPOSTA:
Y
= 3X -4
EXERCÍCIO
–11-
RESPOSTA:
Y = 0 ( É O PRÓPRIO EIXO X)
EXERCÍCIO
–
12 -RESPOSTA:
Y = 6X +5
EXERCÍCIO
–
13- RESPOSTA:
Y = 1 / 6 X + 5 /3
EXERCÍCIO
–
14- RESPOSTA:
Y – 16 = -32 (X + 2)
EXERCÍCIO
–
15 - RESPOSTA:
-1
/ X2
EXERCÍCIO
–
16- RESPOSTA:
-2X
/ X4
EXERCÍCIO
–
17 - RESPOSTA: 2AX
EXERCÍCIO
–
18- RESPOSTA:
-
1 / (X +1)2
EXERCÍCIO
–
19 - RESPOSTA: -1/2 . X -3/2
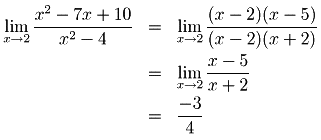
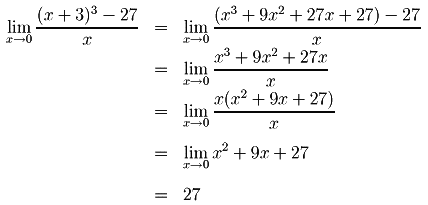
0 comentários:
Postar um comentário